La fracción de neuronas que producen descargas en una gran red neuronal en un momento determinado la llamaremos x. Un modelo simple para el estudio de la epilepsia establece que la dinámica de la red está descrita por la ecuación .
En esta ecuación n significa el número de pasos efectuados desde un cierto estado inicial. Si partimos de una fracción de neuronas conocida, x1= 0,04, podemos calcular x2 sustituyendo en la fórmula, en lugar de n ponemos 1. Los números a y b, llamados parámetros, hay que calcularlos antes.
Por supuesto que este ejemplo es un poco complicado para cuarto o quinto año, pero es sólo un caso real del uso de las sucesiones.
Veamos otra aplicación de las sucesiones, también llamadas progresiones.
La difusión de la gripe en una cierta escuela se modela mediante al ecuación donde

P(t) indica el número total de estudiantes infectados t días despues de observar por primera vez la gripe.
En el primer caso, el de las neuronas, la fórmula nos da un valor a partir del anterior, pero no podemos calcular rapidamente la fracción x34 sin haber calculado antes x33. Estas fórmulas que dan un valor a partir del anterior se llaman fórmulas de recurrencia.
En el caso de la gripe si, tenemos una formula general.
Desde tiempos inmemoriales la humanidad ha tratado de predecir sucesos y acontecimientos.
Si tenemos varios objetos que estan ordenados mediante una ley que no conocemos explicitamente, sentimos curiosidad o necesidad por poder predecir el término seguiente.
Con el nombre de sucesiones o progresiones se les llama a las funciones cuyos valores, las imágenes, los podemos numerar y ordenar en forma correlativa, como los números naturales. Esto es, podemos hablar de un primer elemento o término inicial, un segundo, uno tercero, y asi sucesivamente, siempre que haya una relación que se cumple en forma estricta, siempre, aunque no la conozcamos.
Por ejemplo, si hablamos de los nombres de los alumnos de una clase, ordenados en forma alfabética, tenemos una sucesión: Andrés, Beatriz, Carlos, Carolina, Daniel, .........
En una manada de ciervos se puede predecir la población a lo largo del tiempo, siendo esta una función, entre otras variables, de la cantidad de pasto, que a su vez depende del número de insectos. La población inicial es el primer término, luego el segundo es la población al otro año, y así seguimos.
La cantidad de moscas que habrá en el próximo verano es una función del número de huevos del verano pasado, que a su vez es una función de la cantidad de moscas del verano anterior.
En una piscina que se esta llenando vemos que el nivel sube 2 cm cada 10 minutos. ¿En cuánto tiempo se llenara la piscina? ¿Que datos nos hacen falta?
Un antibiótico en sangre tiene una concentración de 50 microgramos por litro y se metabolizan 4 microgramos por litro por cada hora. ¿Que tiempo pasará hasta eliminarlo totalmente? ¿Que supuestos se están haciendo?
Estos son sólo algunos ejemplos de sucesiones.
Veamos si puedes, en las siguientes sucesiones, tratar de descubrir el quinto término:
1 1/2 1/3 1/4 ?
Mercurio Venus Tierra Marte ?
Do Re Mi Fa ?
13 11 9 7 ?
15 18 21 24 ?
1 2 4 8 ?
Nos ocuparemos aquí de las sucesiones numéricas, y más precisamente de aquellas que tienen una ley de formación. Nos nos ocupemos de las listas de números escritos al azar, que no obedecen ninguna ley ni orden, aunque de esto tambien se ocupa la matemática.
A los términos de una sucesión se los denomina según el lugar que ocupan. Al primer término lo llamamos a1, al segundo a2, al tercero a3, y así en general, al término que ocupa el lugar n lo llamamos an.
Definición: Las sucesiones son funciones de dominio natural.
Por comodidad se acostumbra a empezar en el uno. Entonces el dominio son los números naturales menos el cero.
El dominio es el conjunto de los números naturales positivos y el codominio es el conjunto de los números reales. Por ejemplo los primeros términos de la sucesion f(n) son:
fn
f1 2 2
f2 2+3 5
f3 5+3 8
f4 8+3 11
f5 11+3 14
En el ejemplo anterior se trata de una sucesión aritmética porque cada término difiere del anterior en una cantidad constante llamada diferencia. En este caso, esa constante vale 3.
¿Podremos llegar a una fórmula general de cualquier término? ¿Podremos calcular el término que ocupa el lugar número 101 sin tener que hacerlos todos?
Vamos a escribir de nuevo los términos, pero sin hacer ninguna operación:
fn
f1 2 2
f2 2+3 5
f3 2+3+3 8
f4 2+3+3+3 11
f5 2+3+3+3+3 14
El quinto término, esto es, el 14, ¿cuántas veces tiene incuido el número 3? Respuesta: 4 veces, porque la primera vez no le sumamos nada, y en las demás veces le sumamos el 3.
Entonces, el quinto término es 2 + 4 veces el número que se repite, el 3.
Entonces, el sexto término será 2 + 5 veces el número que se repite, el 3.
Entonces, el término número 101 es 2 + 100 veces el número que se repite, el 3.
Esto es, 2 + 3 x 100= 302.
En general, el término que ocupa el lugar n será an=2 + 3 x (n-1)
a1 al primer término
an al último término
d la diferencia constante
n número de términos
Veamos otro ejercicio como ejemplo: Un eucaliptus mide 2 metros y crece 80 cm por año. ¿Que altura alcanzará dentro de 5 años ?
Respuesta: altura dentro de 5 años = a5 = 2 + (5-1).0.80 = 5,20 metros.
---------------------------------------------------------------------------------------------------
Si cada término se obtiene del anterior multiplicando por una cantidad constante llamada razón, se dice que estamos frente a una sucesion geométrica.
Por ejemplo, vamos a inventar una sucesión geométrica en la cual el primer término es el 5 y cada término se obtendrá multiplicando el anterior por 2.
g1 5 5
g2 5 x 2 10
g3 10 x 2 20
g4 20 x 2 40
g5 40 x 2 80
Para el primer término no hemos multiplicado por 2; para obtener el segundo término hemos multiplicado por 2 una sola vez. Par el tercer término hemos multiplicado por 2, dos veces.
Para el quinto término, hemos multiplicado por 2 cuatro veces.
En general, para el termino n se habran multiplicado n-1 veces.
Repetimos el cuadro sin hacer las operaciones, para verlo mejor y darnos cuenta:
a1 5 5
a2 5 x 2 10
a3 5 x 2 x 2 20
a4 5 x 2 x 2 x 2 40
a5 5 x 2 x 2 x 2 x 2 80
En resumen:
a1 es el primer término
an es el último término o término enésimo
r es la razón, constante
n es el número de términos

Ejercicio 1: Supongamos que en un determinado cultivo la población de bacterias se duplica cada 20 minutos. Escribir la ecuación que nos permite hallar la cantidad de bacterias presentes en un tiempo t cualquiera. Determinar el tiempo necesario para que la cantidad de bacterias sea 500 veces la inicial. ayuda más ayuda solución
Ejercicio 2: Supongamos que se decide modelar la población de moscas de la manera más simple posible: el número de moscas de un verano depende de la cantidad de huevos depositados en el verano anterior, que a su vez depende de la cantidad de moscas vivas en el verano anterior. Así, el número de moscas en un verano es una función del número de moscas en el verano anterior: xn+1 = f(xn) donde xn indica el número de moscas en el verano n. (n = 0, 1, 2, 3, .....) Como el ecosistema es sumamente complicado y las posibles mediciones son imperfectas, no podemos esperar que el modelo así establecido vaya a representar exactamente el número de moscas en cada verano. El gran supuesto que hacemos al establecer un modelo así es que el número de moscas en un verano depende únicamente del número de moscas en el verano anterior. Aunque esto no sea esctrictamente cierto, puede servir para una primer aproximación. Aún resta el problema de la determinación de una función que sea consistente con los datos y con los aspectos biológicos de la reproducción de moscas. Nuestro objetivo es estudiar las variaciones del estado con el tiempo, esto es, la dinámica del sistema.
Se puede comenzar haciento un supuesto simple: por cada mosca de la generación n habrá R moscas en la generación n+1. La ecuación será entonces: xn+1 = R. xn
Al estado x1 se la llama estado inicial.
A partir de ese estado inicial, se pueden obtener los demas estados:

Ejercicio 3: Supongamos que el gobierno decide que el aumento de precios del combustible sea más simple: el precio aumentará el mismo porcentaje todos los meses, para que con esto se amortigüe un poco su efecto. Nuestro objetivo es poder conocer el precio para cualquier tiempo. Estudiar las variaciones del estado con el tiempo, esto es, la dinámica del sistema.
Al precio inicial le llamaremos x1. Por ejemplo, el precio en enero.
A partir de este estado inicial, se pueden obtener los demas precios. Si el aumento mensual es de una 7 %, hay que multiplicar por 1,07. Si el aumento es de un 25%, hay que multiplicar por 1,25. A esta cantidad se la llama R, por razón.

Entonces tenemos:
Pero, ¿ que coincidencia, no ??? El diagrama es el mismo que el anterior.
Ejercicio 4: Sucesion de Fibonacci. Se define por recurrencia asi: cada término es igual que la suma de los dos anteriores. Por ejemplo, si los términos anteriores son el 4 y el 7, el siguiente será el 4+7 = 11. Se puede empezar con cualquier par de números, pero lo mas sencillo es comenzar con 1 y 1. Entonces el siguiente será el 1+1 = 2.
En resumen, la sucesion es 1, 1, 2, 3, 5, 8, 13, 22, ...........
Esta sucesión no es geométrica ni aritmética, como tantas otras.
Veamos lo mismo en un "idioma más matemático", mas formal:

¿Podrías escribir los primeros 10 términos de la suceción de Fibonacci con a1= 3 y a2 = 4 ?
¿Y con a1= 2 y a2 = -1?
¿Y ahora, te animás a buscar la formula general de la sucesión de Fibonacci para un termino general n?
No es fácil. Quizás tengas que consultar material, libros, ......... pedir. ¡AUXILIO!!

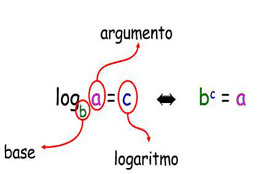
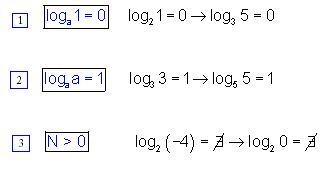
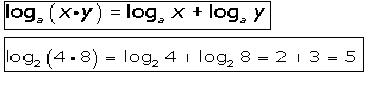

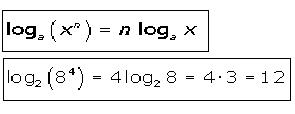






 Si
Si 
